ОБРАЗОВАТЕЛЬНЫЕ: ввести понятие объёма пирамиды, знать их определения, уметь решать задачи на вычисление объёма пирамиды

ВОСПИТАТЕЛЬНЫЕ: воспитать навыки культуры общения, умение слушать и совместно работать с окружающими 

РАЗВИВАЮЩИЕ: развить аналитическое мышление, умение пространственного представления предметов, умение пространственного изображения геометрических фигур, сформировать конструктивный навык построения,  навыки построения пространственных фигур,  аналитическое мышление

ФОРМИРУЕМЫЕ КОМПЕТЕНЦИИ: КК1-коммуникативные компетенции,  КК2- компетенция работы с информацией, КК3- компетенция саморазвития, КК6- компетенция математической грамотности, ПК1- общепредметная математическая компетенция

ТИП УРОКА: комбинированный                                        

МЕТОД УРОКА: повторение пройденного, объяснение нового материала, разминка, «Ответы на вопросы», «скрытые задачи», «кроссворд»

ОБОРУДОВАНИЕ: доска, компьютер, проектор, наглядные и раздаточные материалы

                         

ОРГАНИЗАЦИОННЫЙ МОМЕНТ:  приветствие, проверить готовность класса к уроку, наличие учебных принадлежностей, посещаемость

Повторение пройденного материала: Написать на ватмане цели урока, приготовить медали “умных и  знающих”.

Учитель: 

Сегодня у нас необычный урок – игра “Ответы на вопросы ”. На уроке выиграет та команда, которая лучше училась в течении четверти. Все задания и вопросы будут по пройденному материалу. Поэтому проще выиграть будет тем, кто учил все правила, теоремы, выполнял домашние работы и внимательно слушал на уроках. Но, конечно, победа зависит и от вашей удачи. Для начала выберем капитана команды и приступаем к игре.

“Ответы на вопросы” 

Учитель:

Первая часть – это разминка. Каждой команде предлагается по 15 вопросов. За каждый правильный ответ присуждается 1 балл. Вопросы читаются сначала одной команде, затем другой. Когда вопрос прочитан, тот, кто знает правильный ответ поднимает руку, а капитан называет имя того, кто имеет право ответить. Один и тот же ученик может  отвечать только на 2 вопроса. 

Вопросы 1-ой команде: 

Вопросы 2-й команде: 

 

    2-ая часть “Скрытые задачи” 

Учитель: 

Переходим к следующей части. Вот в нем вам может помочь удача. В мешочке находятся 9 бочонков. Каждый из 8 номеров соответствует номеру задачи, которую вам нужно будет решить. Вытаскивать “задачи” начинает команда, которая проигрывает. После прочтения задачи у команды есть 1 минута на совещание, после этого она дает ответ. Если ответили верно, то прибавляется 2 балла. Если же ответ не верный, то ответить могут соперники, но они за верный ответ получают только 1 балл. Но наша игра – “Удача”, поэтому в мешочке под 9-ым номером прячется 2 балла. То есть, если вы вытащите “задачу” под номером 9, то без решения задачи получаете 2 балла.

Задачи: 

Найдите диагональ параллелепипеда, если его измерения: 1 см, 2см, 2см. (3)

У параллелепипеда три грани имеют площади 4м?, 2м?, 3м?? Чему равна полная поверхность параллелепипеда? (18м?)

Прямая  призма   стороны основания 6м, 8м и боковое ребро 5м, найдите боковую поверхность призмы? (140м?)

Найдите диагональ параллелепипеда, если его размеры: 2см, 3см, 6см. (7)

Найдите полную поверхность правильной четырехугольной призмы, если сторона основания 2см и боковое ребро 5см. (48)

Найдите высоту правильной треугольной пирамиды, если боковое ребро 5см , сторона основания 3см. (4)

Найдите полную поверхность параллелепипеда, если площади граней равны 5м?, 6м?, 4м?. (30м²)

Найдите высоту правильной пятиугольной призмы , если площадь боковой поверхности 50м², боковое ребро 5м. (2м)

После проведения гейма подсчитываются общие баллы.

Следующая часть “Гонка за лидером” 

Учитель:

Ну, а теперь заключительный гейм: “ Гонка за лидером”. Командам даются кроссворды, за каждый верный ответ 1 балл. 

 

Вопросы кроссворда:

По горизонтали: 

1. Есть у любого слова, у растения, и может быть , у уравнения.

По вертикали: 

Подсчитываются баллы. Разбираются вопросы, на которые были даны неправильные ответы.

 

   Новая тема объясняется на слайдах с помощью компьютера и проектора.

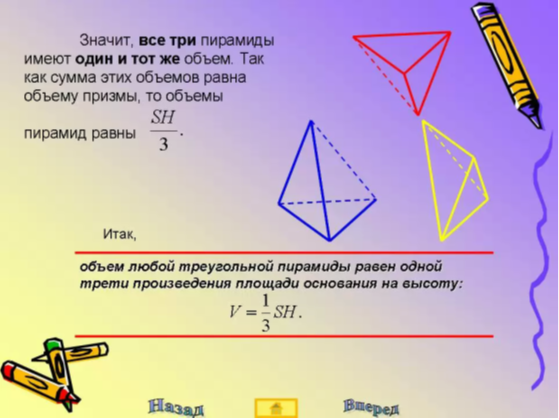
   ТЕОРЕМА.  Объём треугольной пирамиды равен одной трети произведения площади её основания на высоту: 

     ДОКАЗАТЕЛЬСТВО.  Пусть  ОАВС – треугольная пирамида с вершиной  О  и о снованием АВС, высота которой равна  H, а площадь основания  S.

     Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма составлена из данной пирамиды и еще двух пирамид  ОСС₁  В₁  и  ОСВВ ₁.  Пирамиды    ОСС₁  В₁  и  ОСВВ ₁ имеют общую высоту и их основания   СС₁  В₁  и  В ₁ВС являются равными треугольниками. Поэтому их объемы также равны. 

     Аналогично пирамиды  ОАВС и ОСВВ₁ имеют общую высоту, опущенную и вершины С, их основания ОАВ и ВВ₁О являются равными треугольниками.

      Значит, все три пирамиды имеют равные объемы. Учитывая, что сумма их объемов равно объему призмы, получим, что объем треугольной пирамиды  ОАВС будет равен: V =  S_осн *H .

ТЕОРЕМА. Объём любой пирамиды равен одной трети произведения площади её основания на высоту: 

 

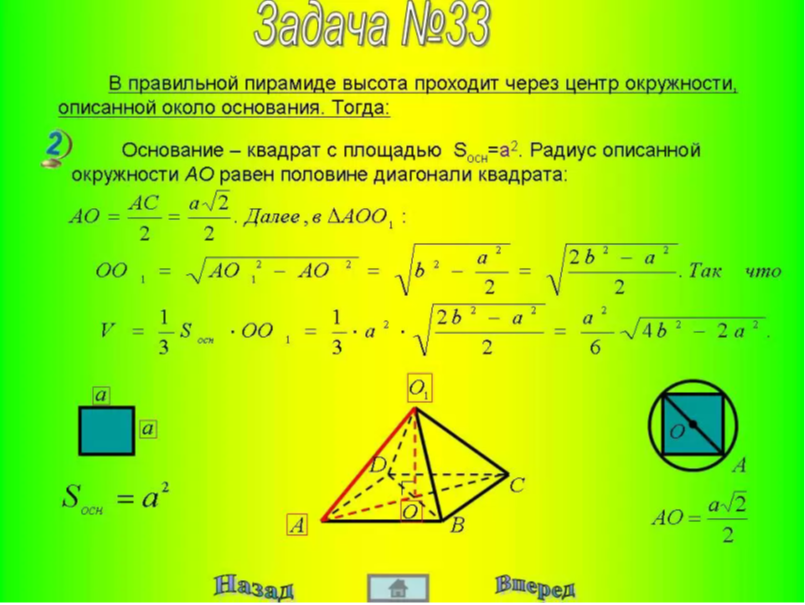
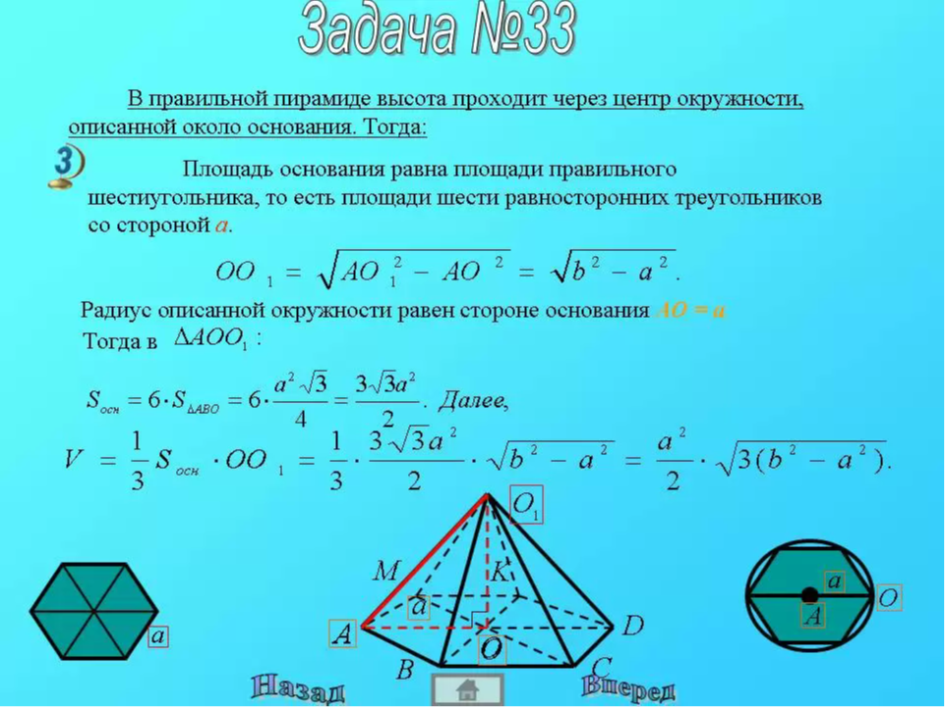
 Работа по учебнику. Решение некоторых задач посмотрим на слайдах:

  

  

  

     

                    

 

Домашнее задание : повторить пройденный  материал, решить задачи №38, № 39 по учебнику.